[When Speed << c]
Till the end 19th century, when electrical science research were on peak, different pioneer came up with analysis that a charged body moving will gain mass.
 | J J Thomson was the first to come up with the idea of increase of mass of moving charged body when moving in space. Most electrical pioneers were mostly mathematical with very hotchpotch physical theory. Faraday tubes are cylindrical vortex filaments extending from one atom to another. He made quantized electricity in to “physical” entity with once single concept called Faraday Tubes, which itself extends from the actual works of Faraday. He rejected Maxwell’s mathematical theory and took a physical approach, through empirically same as that of Maxwell. But different physical meaning. |
He showed that magnetic field is due to motion of faraday tubes. Hence:

\begin{equation}\begin{aligned}\large\overrightarrow{H}=\overrightarrow{v} \times\overrightarrow{D}\end{aligned}\end{equation}
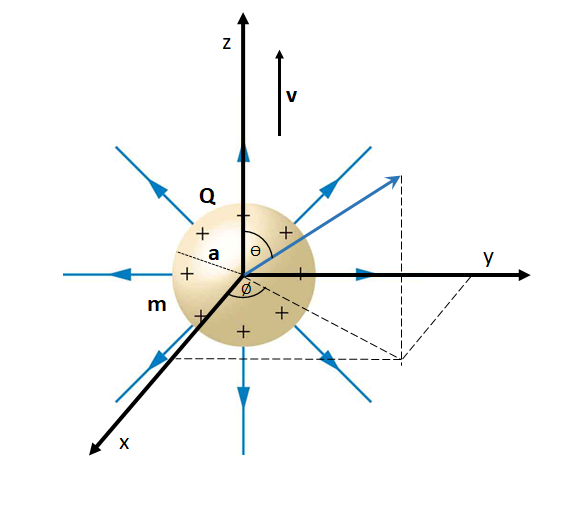
Then the net magnetic field intensity becomes:
\begin{equation}\begin{aligned}\large \overrightarrow{H}& =\overrightarrow{v} \times\overrightarrow{D} \\& = vD\sin\theta \\& = v \epsilon E\sin\theta \end{aligned}\end{equation} Hence, from eqn(2) and eqn(3), we have:
\begin{equation}\begin{aligned}\large H = \frac{v Q \sin\theta}{4\pi r^{2}}\end{aligned}\end{equation}The kinetic energy of the moving sphere is the net magnetic energy per unit volume in the system, which is given as:
\large K.E = \frac{\mu}{2}\left| H \right|^{2}Now to get the total magnetic energy, we shall integrate the above expression over spherical coordinate system, as:
Need to integrate over the entire space from the surface of sphere with radius a to infinity.
So,\begin{aligned}\large K.E & = \large\frac{\mu v^{2}Q^{2}}{32 \pi^{2}}\int_{0}^{2 \pi}\int_{0}^{\pi}\int_{a}^{\infty }\frac{ \sin^{3}\theta}{r^{2}} \partial r \partial \theta \partial \phi \\ & = \large \frac{\mu v^{2}Q^{2}(2\pi)}{32 \pi^{2}}\int_{0}^{\pi}\int_{a}^{\infty }\frac{ \sin^{3}\theta}{r^{2}} \partial r \partial \theta \\ & = \large \frac{\mu v^{2}Q^{2}}{8 \pi}\left[\frac{-1}{r} \right]^{\infty }_{a}\int_{0}^{\pi}\sin^{3}\theta \partial \theta \\ & = \large \frac{\mu v^{2}Q^{2}}{8 \pi a}\int_{0}^{\pi} \frac{1}{4}(\sin3\theta - 3\sin\theta)\partial \theta \end{aligned}Hence integrating we get the final electrical(magnetic) kinetic energy of the moving charge object as:
\begin{aligned}\large K.E_{E} = \frac{\mu}{4\pi}\frac{Q^{2}v^{2}}{3a}\end{aligned}Now if the mass of the object is m, the mechanical kinetic energy is given as:
\begin{aligned}\large K.E_{M} = \frac{1}{2}mv^{2}\end{aligned}If M is the apparent mass of the object on motion through the aether, the total kinetic energy is given by:
\begin{aligned}\large K.E = K.E_{M} + K.E_{E} \\ \large or, \frac{1}{2}Mv^{2} = \frac{1}{2}mv^{2} + \frac{\mu}{4\pi}\frac{Q^{2}}{3a} \\ \large or, M = m + \frac{\mu}{2\pi}\frac{Q^{2}}{3a} \end{aligned}