Impact on Mass of A Moving Charged Object – Part 2

[When Speed → c]

In previous post we have seen how the mass increase for a moving charged object and calculated the value when it’s speed is very less compared to that of light.
https://www.parthasarathimishra.com/wordpress/index.php/2024/02/27/impact-on-mass-of-a-moving-charged-object/

Now we will take a much deeper and detailed analysis for a charged body on how it’s electric field distorts based on speed as first devised by J J Thomson.

The magnetic energy per unit volume of the system is given as:

\large K.E = \frac{\mu}{2}\left| H \right|^{2}\: \: \: \: \: \: \: \: \small------(1)

The electrostatic energy per unit volume is given as:

\large P.E = \frac{\epsilon }{2}\left| E \right|^{2}\: \: \: \: \: \: \: \: \small------(2)

Total energy of the system shall remain constant, hence:

\large P.E + K.E = Constant

Taking derivative with respect to E:

\large \frac{\partial }{\partial \overrightarrow{E}}(P.E) + \frac{\partial }{\partial \overrightarrow{E}}(K.E) = \frac{\partial }{\partial \overrightarrow{E}}(Constant)

\small \frac{\partial }{\partial \overrightarrow{E}}(P.E) + \frac{\partial }{\partial \overrightarrow{E}}(K.E) = \frac{\partial }{\partial \overrightarrow{E}}(Constant)

\large or, \frac{\partial }{\partial \overrightarrow{E}}(\frac{\epsilon }{2}\left| E \right|^{2}) + \frac{\partial }{\partial \overrightarrow{E}}(\frac{\mu}{2}\left| H \right|^{2}) = 0

\small or, \frac{\partial }{\partial \overrightarrow{E}}(\frac{\epsilon }{2}\left| E \right|^{2}) + \frac{\partial }{\partial \overrightarrow{E}}(\frac{\mu}{2}\left| H \right|^{2}) = 0

\large or, -\epsilon \overrightarrow{E} + \mu H\frac{\partial }{\partial \overrightarrow{E}}(\overrightarrow{v} \times \overrightarrow{D}) = 0 \:\:\:\:[\small as, \overrightarrow{H} = \overrightarrow{v} \times \overrightarrow{D}]

\small or, -\epsilon \overrightarrow{E} + \mu H\frac{\partial }{\partial \overrightarrow{E}}(\overrightarrow{v} \times \overrightarrow{D}) = 0 \:\:\:\:[\small as, \overrightarrow{H} = \overrightarrow{v} \times \overrightarrow{D}]

As, as kinetic energy is increasing, hence potential energy shall decrease. So the rate of change of potential energy shall be negative.

Hence, \large -\epsilon \overrightarrow{E} + \mu \epsilon H\frac{\partial }{\partial \overrightarrow{E}}(\overrightarrow{v} \times \overrightarrow{E}) = 0 \:\:\:\:[\small as, \overrightarrow{D} = \epsilon \overrightarrow{E}]

Hence,\\ \small -\epsilon \overrightarrow{E} + \mu \epsilon H\frac{\partial }{\partial \overrightarrow{E}}(\overrightarrow{v} \times \overrightarrow{E}) = 0 \:\:\:\:[\small as, \overrightarrow{D} = \epsilon \overrightarrow{E}]

\large or, \overrightarrow{E} = B\frac{\partial }{\partial \overrightarrow{E}}(\overrightarrow{v} \times \overrightarrow{E}) = 0 \:\:\:\:[\small as, \overrightarrow{B} = \mu \overrightarrow{H}]

To find the derivative of v x E, lets write each vector in its component form and calculate the cross product.

We have:

\large \overrightarrow{v} = v_{x}\hat{i}+v_{y}\hat{j}+v_{z}\hat{k},\: \small\: and, \:\large \overrightarrow{E} = E_{x}\hat{i}+E_{y}\hat{j}+E_{z}\hat{k}

\small \overrightarrow{v} = v_{x}\hat{i}+v_{y}\hat{j}+v_{z}\hat{k},\: \small\: \\ and, \:\small \overrightarrow{E} = E_{x}\hat{i}+E_{y}\hat{j}+E_{z}\hat{k}

\large So, \overrightarrow{v} \times \overrightarrow{E} = (v_{y}E_{z} - E_{y}v_{z})\hat{i} + (E_{x}v_{z} - v_{x}E_{z})\hat{j} + (v_{x}E_{y} - E_{x}v_{y})\hat{k}

\small So, \overrightarrow{v} \times \overrightarrow{E} = \\ \small (v_{y}E_{z} - E_{y}v_{z})\hat{i} + (E_{x}v_{z} - v_{x}E_{z})\hat{j} + (v_{x}E_{y} - E_{x}v_{y})\hat{k}

\large Hence,\:\: B\frac{\partial }{\partial \overrightarrow{E}}(\overrightarrow{v} \times \overrightarrow{E}) = B\frac{\partial }{\partial E_{x}}(\overrightarrow{v} \times \overrightarrow{E})\hat{i} + B\frac{\partial }{\partial E_{y}}(\overrightarrow{v} \times \overrightarrow{E})\hat{j} \\ \large + B\frac{\partial }{\partial E_{z}}(\overrightarrow{v} \times \overrightarrow{E})\hat{k}

\small Hence,\:\: B\frac{\partial }{\partial \overrightarrow{E}}(\overrightarrow{v} \times \overrightarrow{E}) = B\frac{\partial }{\partial E_{x}}(\overrightarrow{v} \times \overrightarrow{E})\hat{i} \\ \small + B\frac{\partial }{\partial E_{y}}(\overrightarrow{v} \times \overrightarrow{E})\hat{j} + B\frac{\partial }{\partial E_{z}}(\overrightarrow{v} \times \overrightarrow{E})\hat{k}

\large \begin{align*} \large &= (Bv_{z} - Bv_{y})\hat{i} + (Bv_{x} - Bv_{z})\hat{j} + (Bv_{y} - Bv_{x})\hat{k} \\ &= \overrightarrow{B}\times \overrightarrow{v}\end{align*}

\small \begin{align*} \small &= (Bv_{z} - Bv_{y})\hat{i} + (Bv_{x} - Bv_{z})\hat{j} + (Bv_{y} - Bv_{x})\hat{k} \\ &= \overrightarrow{B}\times \overrightarrow{v}\end{align*}

\begin{align*} \large So, \:\overrightarrow{E_{1}}=\overrightarrow{B} \times \overrightarrow{v}\end{align*}

This is the electric field intensity due to motional charge. Let’s call it E₁ . Let’s E₂ be the electric field in space due to the electric scalar potential Φ. Such that:

\large \overrightarrow{E_{2}}=-\overrightarrow{\nabla} \phi

The scalar potential can be zero in closed loop, but not in our case.

The total electric field intensity in space for the system is given as (E₁ + E₂):

\large \overrightarrow{E}=(\overrightarrow{B}\times \overrightarrow{v}) \:- \:\overrightarrow{\nabla} \phi

Now lets say a charged object of surface charge Q and radius a moving with a velocity v in the direction of z-axis, for the sake of simplicity.

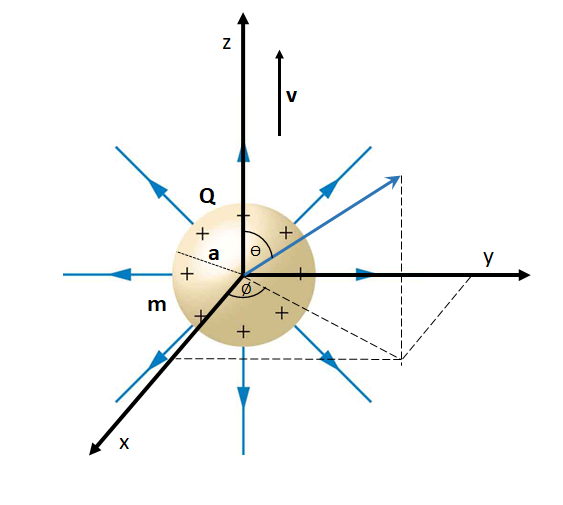
The velocity vector v becomes $\large \overrightarrow{v}=v_{z} \hat{k}$

Now $\large \begin{align*}\overrightarrow{B}=\mu \overrightarrow{H}&= \mu(\overrightarrow{v} \times \overrightarrow{D}) \\ &= \mu[v_{z}\hat{k} \times (D_{x}\hat{i}+D_{y}\hat{j}+D_{z}\hat{k})] \\ &= \mu (-v_{z}D_{y}\hat{i}+v_{z}D_{x}\hat{j})\: \: \: \: \: \: \: \: \small------(3)\end{align*}$

Now $\small \begin{align*}\overrightarrow{B}=\mu \overrightarrow{H}&= \mu(\overrightarrow{v} \times \overrightarrow{D}) \\ \small &= \mu[v_{z}\hat{k} \times (D_{x}\hat{i}+D_{y}\hat{j}+D_{z}\hat{k})] \\ \small &= \mu (-v_{z}D_{y}\hat{i}+v_{z}D_{x}\hat{j})\: \: \: \: \: \: \: \: \small------(3)\end{align*}$

Now the electric field intensity E becomes:

\large \begin{align*}\overrightarrow{E}&=(\overrightarrow{B}\times \overrightarrow{v}) \:- \:\overrightarrow{\nabla} \phi \\ &= [\mu (-v_{z}D_{y}\hat{i}+v_{z}D_{x}\hat{j}) \times v_{z}\hat{k}]\: - \: \overrightarrow{\nabla} \phi \\ &= \mu(v_{z}^{2}D_{x}\hat{i}+v_{z}^{2}D_{y}\hat{j})\:-\: \overrightarrow{\nabla} \phi\end{align*}

Hence $\large \begin{align*}\frac{\overrightarrow{D}}{\epsilon} &= \mu(v_{z}^{2}D_{x}\hat{i}+v_{z}^{2}D_{y}\hat{j})- \overrightarrow{\nabla} \phi\end{align*}$

Or, $\large \begin{align*}\overrightarrow{D} &= \mu \epsilon(v_{z}^{2}D_{x}\hat{i}+v_{z}^{2}D_{y}\hat{j})- \epsilon\overrightarrow{\nabla} \phi \\ &= \frac{v_{z}^{2}}{c^{2}}(D_{x}\hat{i}+D_{y}\hat{j})- \epsilon\overrightarrow{\nabla} \phi \:\:\:\:\:\small[\mu \epsilon =\frac{1}{c^{2}}] \end{align*}$

Now, $\large (D_{x}\hat{i}+D_{y}\hat{j}+D_{z}\hat{k}) = \frac{v_{z}^{2}}{c^{2}}(D_{x}\hat{i}+D_{y}\hat{j})- \epsilon\overrightarrow{\nabla} \phi \\ or,\:\large D_{x}(1-\frac{v_{z}^{2}}{c^{2}})\hat{i} + D_{y}(1-\frac{v_{z}^{2}}{c^{2}})\hat{j} + D_{z}\hat{k} = - \epsilon\overrightarrow{\nabla} \phi$

Now, $\small (D_{x}\hat{i}+D_{y}\hat{j}+D_{z}\hat{k}) = \frac{v_{z}^{2}}{c^{2}}(D_{x}\hat{i}+D_{y}\hat{j})- \epsilon\overrightarrow{\nabla} \phi \\ or,\:\small D_{x}(1-\frac{v_{z}^{2}}{c^{2}})\hat{i} + D_{y}(1-\frac{v_{z}^{2}}{c^{2}})\hat{j} + D_{z}\hat{k} = - \epsilon\overrightarrow{\nabla} \phi$

Splitting the above equation for D into components we get:

\large D_{x}(1-\frac{v_{z}^{2}}{c^{2}}) = - \epsilon\frac{\partial \phi }{\partial x} \\ \: \: \: \: \: \: or, \: \: \: \: \: \:\:\large D_{x} = - (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial x}\: \: \: \: \: \: \:\: \small---(4)

\small D_{x}(1-\frac{v_{z}^{2}}{c^{2}}) = - \epsilon\frac{\partial \phi }{\partial x} \\ \: \: \: \: \: \: or, \: \: \: \: \: \:\:\small D_{x} = - (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial x}\: \: \: \: \: \: \:\: \small---(4)

Similarly, \:\large D_{y} = - (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial y}\: \: \: \: \: \: \: \: \small---(5)

Similarly, \:\small D_{y} = - (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial y}\: \: \: \: \: \: \: \: \small---(5)

\: \: \: \: And, \:\: \: \: \: \: \:\large D_{z} = - \epsilon\frac{\partial \phi }{\partial z}\: \: \: \: \: \: \: \: \:\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \:\small---(6)

\: \: \: \: And, \:\: \: \: \: \: \:\small D_{z} = - \epsilon\frac{\partial \phi }{\partial z}\: \: \: \: \: \: \: \: \:\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \:\small---(6)

Putting the vector components together we get:

\large D_{x}\hat{i}+D_{y}\hat{j}+D_{z}\hat{k} = - (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial x}\hat{i}- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial y}\hat{j}- \epsilon\frac{\partial \phi }{\partial z}\hat{k}

\small D_{x}\hat{i}+D_{y}\hat{j}+D_{z}\hat{k} = - (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial x}\hat{i} \\ - (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial y}\hat{j} - \epsilon\frac{\partial \phi }{\partial z}\hat{k}

or,\: \large \overrightarrow{D} = - (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial x}\hat{i}- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial y}\hat{j}- \epsilon\frac{\partial \phi }{\partial z}\hat{k}

or,\: \small \overrightarrow{D} = - (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial x}\hat{i}- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial y}\hat{j}- \epsilon\frac{\partial \phi }{\partial z}\hat{k}

Now taking divergent both sides:

\: \large \overrightarrow{\nabla }.\overrightarrow{D} = \overrightarrow{\nabla }.[- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial x}\hat{i}- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial y}\hat{j}- \epsilon\frac{\partial \phi }{\partial z}\hat{k}]

\: \small \overrightarrow{\nabla }.\overrightarrow{D} = \overrightarrow{\nabla }.[- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial x}\hat{i}- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial y}\hat{j} \\ \small - \epsilon\frac{\partial \phi }{\partial z}\hat{k}]

As we are dealing with field in space, hence no charge is established there, so the divergence of D should be 0. Hence:

\large \overrightarrow{\nabla }.[- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial x}\hat{i}- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial y}\hat{j}- \epsilon\frac{\partial \phi }{\partial z}\hat{k}] = 0

\small \overrightarrow{\nabla }.[- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial x}\hat{i}- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\epsilon\frac{\partial \phi }{\partial y}\hat{j}- \epsilon\frac{\partial \phi }{\partial z}\hat{k}] = 0

or\:\: \large - (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\frac{\partial^{2} \phi }{\partial x^{2}}- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\frac{\partial^{2} \phi }{\partial y^{2}}- \frac{\partial^{2} \phi }{\partial z^{2}} = 0

or\:\: \small - (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\frac{\partial^{2} \phi }{\partial x^{2}}- (\frac{c^{2}}{{c^{2}}-v_{z}^{2}})\frac{\partial^{2} \phi }{\partial y^{2}}- \frac{\partial^{2} \phi }{\partial z^{2}} = 0

or\:\: \large \frac{\partial^{2} \phi }{\partial x^{2}}+\frac{\partial^{2} \phi }{\partial y^{2}}+(\frac{{c^{2}}-v_{z}^{2}}{c^{2}}) \frac{\partial^{2} \phi }{\partial z^{2}} = 0\: \: \: \: \: \: \: \: \: \: \: \:\small---(7)

or\:\: \small \frac{\partial^{2} \phi }{\partial x^{2}}+\frac{\partial^{2} \phi }{\partial y^{2}}+(\frac{{c^{2}}-v_{z}^{2}}{c^{2}}) \frac{\partial^{2} \phi }{\partial z^{2}} = 0\: \: \: \: \: \: \: \: \: \: \: \:\small---(7)

Now to solve this equation, we have to do coordinate transform of Z axis.

Lets put:

\large z'=\frac{c}{\sqrt{c^{2}-v_{z}^{2}}}z

Using chain rule: $\large \frac{\partial\phi}{\partial z'} = \frac{\partial\phi}{\partial z}\frac{\partial z}{\partial z'} \\ \begin{align*}or,\:\large \frac{\partial^{2}\phi}{\partial z'^{2}} &= \frac{\partial\phi}{\partial z}\frac{\partial z}{\partial z'}\frac{\partial z}{\partial z'} \\ &= \frac{\partial^{2}\phi}{\partial z^{2}}(\frac{\partial z}{\partial z'})^{2} \\ &=(\frac{{c^{2}}-v_{z}^{2}}{c^{2}})\frac{\partial^{2}\phi}{\partial z^{2}}\end{align*}$

Now eqn(7) becomes: $\large \frac{\partial^{2} \phi }{\partial x^{2}}+\frac{\partial^{2} \phi }{\partial y^{2}}+\frac{\partial^{2} \phi }{\partial z'^{2}} = 0$

Now this is Laplace equation for potential. Following is the standard solution for electric potential:

\begin{align*}\large \phi &= \large \frac{A}{\sqrt{x^{2}+y^{2}+z'^{2}}} \\ &= \large \frac{A}{\sqrt{x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2}}}\end{align*}

To find the constant A, we need to first find gradient of the scalar potential Φ and find the Displacement D, and then integrate the Displacement over entire surface of the sphere and equate with the net charge Q as per Gauss law.

The gradient of scalar potential, ∇.Φ is:

\large \frac{\partial \phi}{\partial x} = \frac{-Ax}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}

\large \frac{\partial \phi}{\partial y} = \frac{-Ay}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}

\large \frac{\partial \phi}{\partial z} = \frac{c^{2}}{(c^{2}-v_{z}^{2})}\frac{-Az}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}

Now putting the value of components of gradient of potential in eqn(4), (5) and (6), we get:

\large D_{x} = \frac{c^{2}}{(c^{2}-v_{z}^{2})}\frac{\epsilon Ax}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}\: \: \: \: \: \: \: \: \: \: \: \:\small---(8)

\small D_{x} = \frac{c^{2}}{(c^{2}-v_{z}^{2})}\frac{\epsilon Ax}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}\: \: \: \: \: \: \: \: \:\small---(8)

\large D_{y} = \frac{c^{2}}{(c^{2}-v_{z}^{2})}\frac{\epsilon Ay}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}\: \: \: \: \: \: \: \: \: \: \: \:\small---(9)

\small D_{y} = \frac{c^{2}}{(c^{2}-v_{z}^{2})}\frac{\epsilon Ay}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}\: \: \: \: \: \: \: \: \:\small---(9)

\large D_{z} = \frac{c^{2}}{(c^{2}-v_{z}^{2})}\frac{\epsilon Az}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}\: \: \: \: \: \: \: \: \: \: \: \:\small---(10)

\small D_{z} = \frac{c^{2}}{(c^{2}-v_{z}^{2})}\frac{\epsilon Az}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}\: \: \: \: \: \: \: \: \:\small---(10)

Now according to Gauss law of electrostatics, the total electric displacement across a surface of a charged object is always the amount of charge contained.

\large \oiint \overrightarrow{D}.\hat{n}\:dS = Q\: \: \: \: \: \: \: \: \: \: \: \:\: \: \: \: \: \: \: \: \: \:\small---(11)

The normal unit vector n for the sphere with radius a is defined as:

\large \hat{n} = \frac{x}{a}\hat{i}+\frac{y}{a}\hat{j}+\frac{z}{a}\hat{k}

Now integral (11) becomes:

\begin{align*} \large Q &= \large \frac{\epsilon A c^{2}}{(c^{2}-v^{2}_{z})}\oiint(\frac{x\hat{i}+y\hat{j}+z\hat{k}}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}).(\frac{x}{a}\hat{i}+\frac{y}{a}\hat{j}+\frac{z}{a}\hat{k})dS \\ &= \large \frac{\epsilon A c^{2}}{a(c^{2}-v^{2}_{z})}\oiint\frac{x^{2}+y^{2}+z^{2}}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}dS \\ &= \large \frac{\epsilon a A c^{2}}{(c^{2}-v^{2}_{z})}\oiint\frac{dS}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}} \:\:\:\:\:\:\:\:\:\:\:\: \small[as, x^{2}+y^{2}+z^{2}=a^{2}]\end{align*}

\begin{align*} \small Q &= \small \frac{\epsilon A c^{2}}{(c^{2}-v^{2}_{z})}\oiint(\tiny \frac{x\hat{i}+y\hat{j}+z\hat{k}}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}).(\frac{x}{a}\hat{i}+\frac{y}{a}\hat{j}+\frac{z}{a}\hat{k} \small )dS \\ &= \small \frac{\epsilon A c^{2}}{a(c^{2}-v^{2}_{z})}\oiint\frac{x^{2}+y^{2}+z^{2}}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}}dS \\ &= \small \frac{\epsilon a A c^{2}}{(c^{2}-v^{2}_{z})}\oiint\frac{dS}{(x^{2}+y^{2}+(\frac{c^{2}}{c^{2}-v_{z}^{2}})z^{2})^{\frac{3}{2}}} \\ & \large [as, x^{2}+y^{2}+z^{2}=a^{2}]\end{align*}

Now for proper evaluation, we need to convert this to spherical coordinate.
So we have: $\large x = rcos\phi sin\theta \\ \large y = rsin\phi sin\theta \\ \large z = rcos\theta \\ \large dS = r^{2}sin\theta d\theta d\phi$

The variable r should be set to radius a as we are not integrating over volume.

So now putting the above expression into the integral we get:

\begin{align*} \large Q &= \small \frac{\epsilon a A c^{2}}{(c^{2}-v^{2}_{z})}\int_{0}^{ \pi}\int_{0}^{2 \pi}\frac{a^{2}sin\theta\: \partial \theta \: \partial \phi}{(a^{2}cos^{2}\phi sin^{2}\theta+a^{2}sin^{2}\phi sin^{2}\theta+(\frac{c^{2}}{c^{2}-v_{z}^{2}})a^{2}cos^{2}\theta)^{\frac{3}{2}}} \\ &= \large \frac{\epsilon A c^{2}}{(c^{2}-v^{2}_{z})}\int_{0}^{ \pi}\int_{0}^{2 \pi}\frac{sin\theta\: \partial \theta \: \partial \phi}{(sin^{2}\theta+(\frac{c^{2}}{c^{2}-v_{z}^{2}})cos^{2}\theta)^{\frac{3}{2}}} \\ &=\large \frac{2 \pi\epsilon A c^{2}}{(c^{2}-v^{2}_{z})}\int_{0}^{ \pi}\frac{sin\theta\: \partial \theta}{(sin^{2}\theta+(\frac{c^{2}}{c^{2}-v_{z}^{2}})cos^{2}\theta)^{\frac{3}{2}}} \\ &= \large \frac{2 \pi\epsilon A c^{2}}{(c^{2}-v^{2}_{z})}\int_{0}^{ \pi}\frac{sin\theta\: \partial \theta}{(1+(\frac{v_{z}^{2}}{c^{2}-v_{z}^{2}})cos^{2}\theta)^{\frac{3}{2}}} \end{align*}

\begin{align*} \small Q &= \tiny \frac{\epsilon a A c^{2}}{(c^{2}-v^{2}_{z})}\small \int_{0}^{ \pi}\int_{0}^{2 \pi}\tiny \frac{a^{2}sin\theta\: \partial \theta \: \partial \phi}{(a^{2}cos^{2}\phi sin^{2}\theta+a^{2}sin^{2}\phi sin^{2}\theta+(\frac{c^{2}}{c^{2}-v_{z}^{2}})a^{2}cos^{2}\theta)^{\frac{3}{2}}} \\ &= \small \frac{\epsilon A c^{2}}{(c^{2}-v^{2}_{z})}\int_{0}^{ \pi}\int_{0}^{2 \pi}\frac{sin\theta\: \partial \theta \: \partial \phi}{(sin^{2}\theta+(\frac{c^{2}}{c^{2}-v_{z}^{2}})cos^{2}\theta)^{\frac{3}{2}}} \\ &=\small \frac{2 \pi\epsilon A c^{2}}{(c^{2}-v^{2}_{z})}\int_{0}^{ \pi}\frac{sin\theta\: \partial \theta}{(sin^{2}\theta+(\frac{c^{2}}{c^{2}-v_{z}^{2}})cos^{2}\theta)^{\frac{3}{2}}} \\ &= \small \frac{2 \pi\epsilon A c^{2}}{(c^{2}-v^{2}_{z})}\int_{0}^{ \pi}\frac{sin\theta\: \partial \theta}{(1+(\frac{v_{z}^{2}}{c^{2}-v_{z}^{2}})cos^{2}\theta)^{\frac{3}{2}}} \end{align*}

Now we solve this integral by substituting: $\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}cos\theta = tan\psi \\ Hence,\: \frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}sin\theta\: \partial\theta = sec^{2}\psi \: \partial \psi$

Now the above integral becomes: $\begin{align*} Q &= \large \frac{2 \pi\epsilon A c^{2}}{(c^{2}-v^{2}_{z})}\int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}\frac{-\sqrt{c^{2}-v_{z}^{2}}}{v_{z}} \frac{sec^{2}\psi}{(1+tan^{2}\psi)^{\frac{3}{2}}} \: \partial \psi \\ &= \large \frac{-2 \pi\epsilon A c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}cos \psi \: \partial \psi \\ &= \large \frac{-2 \pi\epsilon A c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\left[ sin \psi \right]^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} \\ &= \large \frac{-2 \pi\epsilon A c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\left[ \frac{tan \psi}{\sqrt{1+tan^{2}\psi}} \right]^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} \\ &= \large \frac{-2 \pi\epsilon A c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\frac{\frac{-2v_{z}}{\sqrt{c^2-v_{z}^{2}}}}{\sqrt{1+\frac{v_{z}^{2}}{c^{2}-v_{z}^{2}}}} \\ &= \large \frac{4 \pi \epsilon Ac}{\sqrt{c^2-v^2_{z}}} \end{align*}$

Now the above integral becomes: $\begin{align*} Q &= \small \frac{2 \pi\epsilon A c^{2}}{(c^{2}-v^{2}_{z})}\int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}\frac{-\sqrt{c^{2}-v_{z}^{2}}}{v_{z}} \tiny \frac{sec^{2}\psi}{(1+tan^{2}\psi)^{\frac{3}{2}}} \: \small \partial \psi \\ &= \small \frac{-2 \pi\epsilon A c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}cos \psi \: \partial \psi \\ &= \small \frac{-2 \pi\epsilon A c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\left[ sin \psi \right]^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} \\ &= \small \frac{-2 \pi\epsilon A c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\left[ \frac{tan \psi}{\sqrt{1+tan^{2}\psi}} \right]^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} \\ &= \small \frac{-2 \pi\epsilon A c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\frac{\frac{-2v_{z}}{\sqrt{c^2-v_{z}^{2}}}}{\sqrt{1+\frac{v_{z}^{2}}{c^{2}-v_{z}^{2}}}} \\ &= \small \frac{4 \pi \epsilon Ac}{\sqrt{c^2-v^2_{z}}} \end{align*}$

Now A becomes: $\large A = \frac{Q}{4 \pi \epsilon}\frac{\sqrt{c^2-v^2_{z}}}{c}$

Now putting the value of A in scalar potential equation it becomes: $\begin{align*}\large \phi &= \large \frac{Q \sqrt{1 - \frac{v_{z}^{2}}{c^{2}}}}{4 \pi \epsilon \sqrt{x^{2}+y^{2}+\left(\frac{1}{1-\frac{v_{z}^{2}}{c^{2}}}\right)z^{2}}}\end{align*}\: \: \: \: \: \: \: \:\small---(12)$

You can see when the speed approaches speed of light the factor v_z/c becomes prevalent and the potential becomes undefined at that speed.

The potential can be expressed in spherical coordinate as:

\begin{align*}\large \phi &= \large \frac{Q \sqrt{1 - \frac{v_{z}^{2}}{c^{2}}}}{4 \pi \epsilon r\sqrt{sin^{2}\theta + \left(\frac{1}{1-\frac{v_{z}^{2}}{c^{2}}} \right)cos^{2}\theta}}\end{align*}

Now putting the value of A in eqn(8), (9), (10) we get D as:

\large \overrightarrow{D}=\frac{Q}{4 \pi}\frac{1}{\sqrt{1-\frac{v_{z}^{2}}{c^{2}}}}\frac{1}{ (x^{2}+y^{2}+\frac{1}{1-\frac{v_{z}^2}{c^2}}z^{2})^{\frac{3}{2}}}(x\hat{i}+y\hat{j}+z\hat{k})\: \: \: \: \: \: \: \:\small---(13)

\begin{align*} \small \overrightarrow{D} &= \small \frac{Q}{4 \pi}\frac{1}{\sqrt{1-\frac{v_{z}^{2}}{c^{2}}}}\frac{1}{ (x^{2}+y^{2}+\frac{1}{1-\frac{v_{z}^2}{c^2}}z^{2})^{\frac{3}{2}}}(x\hat{i}+y\hat{j}+z\hat{k})\\ & \: \: \: \: \: \: \: \: \: \small---(13)\end{align*}

In spherical coordinate, the D can be expressed as: $\small \overrightarrow{D}=\frac{Q}{4 \pi}\frac{1}{\sqrt{1-\frac{v_{z}^{2}}{c^{2}}}}\frac{1}{ r^{2}(sin^{2}\theta+\frac{1}{1-\frac{v_{z}^2}{c^2}}cos^{2}\theta)^{\frac{3}{2}}} (cos\phi sin \theta\hat{r}+sin \phi sin \theta\hat{\theta}+cos \theta\hat{\phi})$

In spherical coordinate, the D can be expressed as: $\begin{align*} \small \overrightarrow{D} &= \small \frac{Q}{4 \pi}\frac{1}{\sqrt{1-\frac{v_{z}^{2}}{c^{2}}}}\frac{1}{ r^{2}(sin^{2}\theta+\frac{1}{1-\frac{v_{z}^2}{c^2}}cos^{2}\theta)^{\frac{3}{2}}} \\ &\: \: \: \: \: \: \: \: \small (cos\phi sin \theta\hat{r}+sin \phi sin \theta\hat{\theta}+cos \theta\hat{\phi})\end{align*}$

The above equation shows that the the faraday tubes are radial and the resultant polarization D varies inversely as $\large D \propto \frac{1}{r^{2}(sin^{2}\theta+\frac{1}{1-\frac{v_{z}^2}{c^2}}cos^{2}\theta)^{\frac{3}{2}}}$

The result shows that the polarization is greatest when θ=π/2, and least when θ=0. The faraday tubes thus leave the poles of the sphere and tend to crowd at the equator. These is due to the tendencies of tubes to set themselves at right angles to the direction in which they are moving.

The surface charge density is given by multiplying the displacement with normal vector, which is proportional as

\large \overrightarrow{D}.\hat{n} \propto \frac{1}{(sin^{2}\theta+\frac{1}{1-\frac{v_{z}^2}{c^2}}cos^{2}\theta)^{\frac{3}{2}}}

The surface charge density is maximum at equator and minimum at poles.

To plot the potential and displacement, we can convert eqn(12) of potential into two dimensional equation for the sake of simplicity in visualization. We can replace z as x as we can visualize moving in x direction and remove the actual x part. Also the equation is with respect to moving frame. To get the proper field picture, we can transform the x-axis into the stationary from using x → x – vt. Then we can ploy y as:

\large \phi = \large \frac{Q \sqrt{1 - \frac{v_{z}^{2}}{c^{2}}}}{4 \pi \epsilon \sqrt{y^{2}+\left(\frac{1}{1-\frac{v^{2}}{c^{2}}}\right)x^{2}}} \\ or, \: \large y = \pm \sqrt{\frac{Q^2}{\beta ^2 \phi ^2 (4 \pi \epsilon)^2} -\beta ^2 x^2}\:\:\:\:\: \small [where,\: \beta = \frac {1}{\sqrt{1-\frac{v^2}{c^2}}}]

\begin{align*} \small & \phi = \small \frac{Q \sqrt{1 - \frac{v_{z}^{2}}{c^{2}}}}{4 \pi \epsilon \sqrt{y^{2}+\left(\frac{1}{1-\frac{v^{2}}{c^{2}}}\right)x^{2}}} \\ or, \: \large y &= \pm \sqrt{\frac{Q^2}{\beta ^2 \phi ^2 (4 \pi \epsilon)^2} -\beta ^2 x^2} \\ & \:\:\:\:\: \small [where,\: \beta = \frac {1}{\sqrt{1-\frac{v^2}{c^2}}}]\end{align*}

Following are the plot of potential (in gray) and displacement (in blue) for the the charged object when the v =0 and when v = 0.8c.

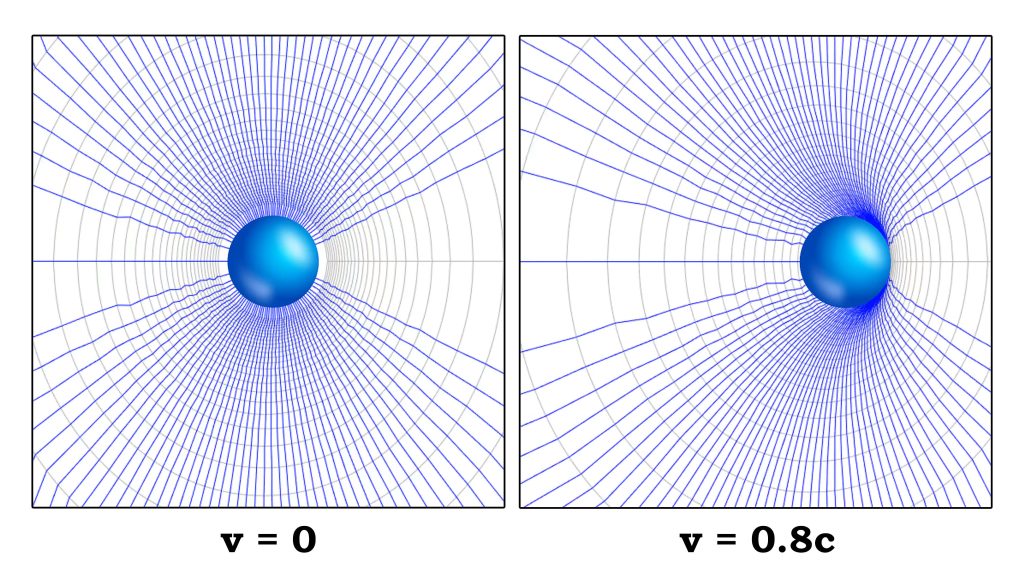
You can clearly see when the speed approach that of light, the field starts to distort as they don’t get enough time to realign, hence compressing the aether. Following is a short visualization with animation.

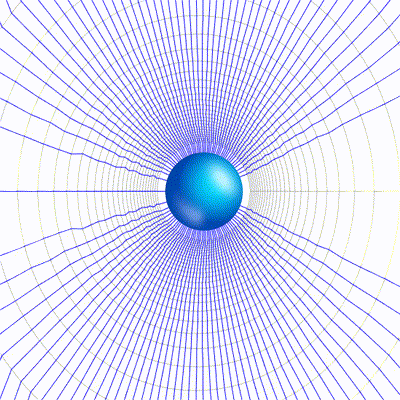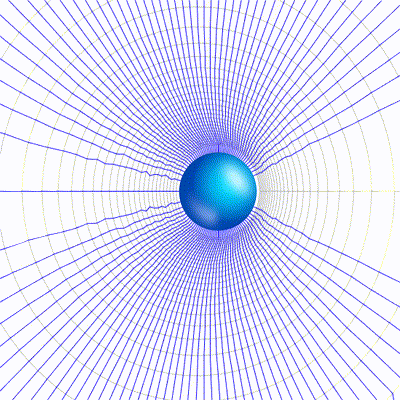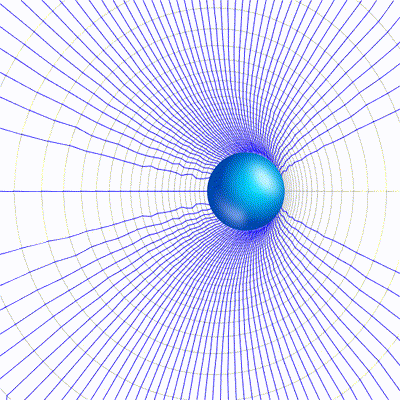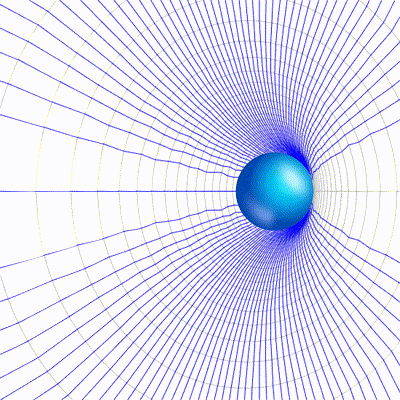
The magnetic field intensity H can be now derived from D using eqn(3), as: $\large \overrightarrow{H}=\frac{Q}{4 \pi}\frac{1}{\sqrt{1-\frac{v_{z}^{2}}{c^{2}}}}\frac{v_{z}}{ (x^{2}+y^{2}+\frac{1}{1-\frac{v_{z}^2}{c^2}}z^{2})^{\frac{3}{2}}}(-y\hat{i}+x\hat{j})$

The magnetic field intensity H can be now derived from D using eqn(3), as: $\small \overrightarrow{H}=\frac{Q}{4 \pi}\frac{1}{\sqrt{1-\frac{v_{z}^{2}}{c^{2}}}}\frac{v_{z}}{ (x^{2}+y^{2}+\frac{1}{1-\frac{v_{z}^2}{c^2}}z^{2})^{\frac{3}{2}}}(-y\hat{i}+x\hat{j})$

The magnetic energy per unit volume is given from eqn(1) as $\large \frac{\mu}{2}\left| H \right|^{2}=\frac{\mu Q^2}{32 \pi^{2}}\frac{1}{(1-\frac{v_{z}^{2}}{c^{2}})}\frac{v_{z}^{2}(x^2+y^{2})}{ (x^{2}+y^{2}+\frac{1}{1-\frac{v_{z}^2}{c^2}}z^{2})^{3}}$

The magnetic energy per unit volume is given from eqn(1) as $\small \frac{\mu}{2}\left| H \right|^{2}=\frac{\mu Q^2}{32 \pi^{2}}\frac{1}{(1-\frac{v_{z}^{2}}{c^{2}})}\frac{v_{z}^{2}(x^2+y^{2})}{ (x^{2}+y^{2}+\frac{1}{1-\frac{v_{z}^2}{c^2}}z^{2})^{3}}$

Converting the kinetic energy per unit volume into spherical coordinate we get: $\large \frac{\mu Q^2}{32 \pi^{2}}\frac{v_{z}^{2}}{(1-\frac{v_{z}^{2}}{c^{2}})}\frac{sin^2\theta}{ r^{4}(sin^{2}\theta+\frac{1}{1-\frac{v_{z}^2}{c^2}}cos^{2}\theta)^{3}}$

To calculate the total kinetic energy we need to integrate the above expression for the entire space after the sphere surface. $\begin{align*}\large K.E &= \large\frac{\mu Q^2}{32 \pi^{2}}\frac{v_{z}^{2}}{(1-\frac{v_{z}^{2}}{c^{2}})}\int_{0}^{2 \pi }\int_{0}^{\pi}\int_{a}^{\infty }\frac{sin^2\theta}{ r^{4}(sin^{2}\theta+\frac{1}{1-\frac{v_{z}^2}{c^2}}cos^{2}\theta)^{3}} r^{2}sin\theta \partial \theta \partial \phi \\ &= \large\frac{\mu Q^2}{16 \pi}\frac{v_{z}^{2}}{(1-\frac{v_{z}^{2}}{c^{2}})}\int_{0}^{\pi}\int_{a}^{\infty }\frac{sin^3\theta}{ r^{2}(sin^{2}\theta+\frac{1}{1-\frac{v_{z}^2}{c^2}}cos^{2}\theta)^{3}} \partial \theta \\ &= \large\frac{\mu Q^2}{16 \pi a}\frac{v_{z}^{2}}{(1-\frac{v_{z}^{2}}{c^{2}})}\int_{0}^{\pi}\frac{sin^3\theta}{ (sin^{2}\theta+\frac{1}{1-\frac{v_{z}^2}{c^2}}cos^{2}\theta)^{3}} \partial \theta \\ &= \large\frac{\mu Q^2}{16 \pi a}\frac{v_{z}^{2}}{(1-\frac{v_{z}^{2}}{c^{2}})}\int_{0}^{\pi}\frac{sin^3\theta}{ (1+\frac{v_{z}^2}{c^{2}-v_{z}^{2}}cos^{2}\theta)^{3}} \partial \theta \end{align*}$

To calculate the total kinetic energy we need to integrate the above expression for the entire space after the sphere surface. $\begin{align*}\small K.E &= \tiny \frac{\mu Q^2}{32 \pi^{2}}\frac{v_{z}^{2}}{(1-\frac{v_{z}^{2}}{c^{2}})} \small \int_{0}^{2 \pi }\int_{0}^{\pi}\int_{a}^{\infty }\tiny \frac{sin^2\theta}{ r^{4}(sin^{2}\theta+\frac{1}{1-\frac{v_{z}^2}{c^2}}cos^{2}\theta)^{3}} r^{2}sin\theta \partial \theta \partial \phi \\ &= \small \frac{\mu Q^2}{16 \pi}\frac{v_{z}^{2}}{(1-\frac{v_{z}^{2}}{c^{2}})}\int_{0}^{\pi}\int_{a}^{\infty }\tiny \frac{sin^3\theta}{ r^{2}(sin^{2}\theta+\frac{1}{1-\frac{v_{z}^2}{c^2}}cos^{2}\theta)^{3}} \small \partial \theta \\ &= \small \frac{\mu Q^2}{16 \pi a}\frac{v_{z}^{2}}{(1-\frac{v_{z}^{2}}{c^{2}})}\int_{0}^{\pi}\frac{sin^3\theta}{ (sin^{2}\theta+\frac{1}{1-\frac{v_{z}^2}{c^2}}cos^{2}\theta)^{3}} \partial \theta \\ &= \small \frac{\mu Q^2}{16 \pi a}\frac{v_{z}^{2}}{(1-\frac{v_{z}^{2}}{c^{2}})}\int_{0}^{\pi}\frac{sin^3\theta}{ (1+\frac{v_{z}^2}{c^{2}-v_{z}^{2}}cos^{2}\theta)^{3}} \partial \theta \end{align*}$

To solve the above integral, let’s set: $cos\theta = u \\ Hence,\: sin\theta\: \partial\theta = - \partial u$

Now the integral becomes: $\begin{align*}\large K.E &=\large\frac{\mu Q^2}{16 \pi a}\frac{v_{z}^{2}}{(1-\frac{v_{z}^{2}}{c^{2}})}\int_{1}^{-1}\frac{u^{2} - 1}{ (1+\frac{v_{z}^2}{c^{2}-v_{z}^{2}}u^{2})^{3}} \partial u \end{align*}$

Now the integral becomes: $\begin{align*}\small K.E &=\small \frac{\mu Q^2}{16 \pi a}\frac{v_{z}^{2}}{(1-\frac{v_{z}^{2}}{c^{2}})}\int_{1}^{-1}\frac{u^{2} - 1}{ (1+\frac{v_{z}^2}{c^{2}-v_{z}^{2}}u^{2})^{3}} \partial u \end{align*}$

Now again set: $\begin{align*}\large \frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}u = tan \psi \\ so, \partial u = \frac{\sqrt{c^{2}-v_{z}^{2}}}{v_{z}}sec^{2}\psi \partial \psi \end{align*}$

Now the integral reduced to: $\begin{align*}\large K.E &=\small\frac{\mu Q^2}{16 \pi a}\frac{1}{(1-\frac{v_{z}^{2}}{c^{2}})}\frac{\sqrt{c^{2}-v_{z}^{2}}}{v_{z}}\int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} ((c^{2}-v_{z}^{2})sin^{2}\psi cos^{2}\psi - v_{z}^{2}cos^{4}\psi) \partial \psi \\ &= \small\frac{\mu Q^2}{16 \pi a}\frac{1}{(1-\frac{v_{z}^{2}}{c^{2}})}\frac{\sqrt{c^{2}-v_{z}^{2}}}{v_{z}}\int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} (c^{2}sin^{2}\psi cos^{2}\psi - v_{z}^{2}cos^{2}\psi) \partial \psi \\ &= \small\frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}}\int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} (\frac{c^{2}}{v_{z}^{2}}sin^{2}\psi cos^{2}\psi - cos^{2}\psi) \partial \psi \\ &= \small\frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}}\int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} (\frac{c^{2}}{v_{z}^{2}}\frac{1}{8}(1 - cos4 \psi) - \frac{1}{2}(1 + cos 2 \psi)) \partial \psi \\ &= \small\frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}} \left[ \frac{c^{2}}{v_{z}^{2}}\frac{1}{8}(\psi - \frac{sin 4 \psi}{4}) - \frac{1}{2}(\psi + \frac{sin 2\psi}{2}) \right]^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} \\ &= \small\frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}} \left[ \frac{c^{2}}{8v_{z}^{2}}\psi - \frac{c^{2}}{8v_{z}^{2}}\frac{sin 4\psi}{4} - \frac{\psi}{2} -\frac{sin 2 \psi}{4}\right]^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} \end{align*}$

Now the integral reduced to: $\begin{align*}\large K.E &=\tiny \frac{\mu Q^2}{16 \pi a}\frac{1}{(1-\frac{v_{z}^{2}}{c^{2}})}\frac{\sqrt{c^{2}-v_{z}^{2}}}{v_{z}}\small \int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}\tiny ((c^{2}-v_{z}^{2})sin^{2}\psi cos^{2}\psi \\ & \:\:\:\:\:\:\:\:\:\: \tiny - v_{z}^{2}cos^{4}\psi) \partial \psi \\ &= \tiny \frac{\mu Q^2}{16 \pi a}\frac{1}{(1-\frac{v_{z}^{2}}{c^{2}})}\frac{\sqrt{c^{2}-v_{z}^{2}}}{v_{z}}\small \int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} \tiny (c^{2}sin^{2}\psi cos^{2}\psi \\ & \:\:\:\:\:\:\:\:\:\: \tiny - v_{z}^{2}cos^{2}\psi) \partial \psi \\ &= \tiny \frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}}\small \int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} \tiny (\frac{c^{2}}{v_{z}^{2}}sin^{2}\psi cos^{2}\psi - cos^{2}\psi) \partial \psi \\ &= \tiny \frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}}\small \int_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} \tiny(\frac{c^{2}}{v_{z}^{2}}\frac{1}{8}(1 - cos4 \psi) \\ & \:\:\:\:\:\:\:\:\:\: \tiny - \frac{1}{2}(1 + cos 2 \psi)) \partial \psi \\ &= \tiny \frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}} \left[ \frac{c^{2}}{v_{z}^{2}}\frac{1}{8}(\psi - \frac{sin 4 \psi}{4}) - \frac{1}{2}(\psi + \frac{sin 2\psi}{2}) \right]^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} \\ &= \tiny \frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}} \left[ \frac{c^{2}}{8v_{z}^{2}}\psi - \frac{c^{2}}{8v_{z}^{2}}\frac{sin 4\psi}{4} - \frac{\psi}{2} -\frac{sin 2 \psi}{4}\right]^{tan^{-1}\frac{-v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}}_{tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}} \end{align*}$

By substituting: $\large tan^{-1}\frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}} = v_{2}$ the above equation reduced to:

\large K.E = \large \frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}}\left[ v_{2}(1 - \frac{c^{2}}{4v_{z}^{2}}) + \frac{1}{2}sin 2v_{2}(1+\frac{c^2}{4v_{z}^{2}}cos2v_{2}) \right]

\begin{align*} \small K.E &= \small \frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}}[ v_{2}(1 - \frac{c^{2}}{4v_{z}^{2}}) \\ & \:\:\:\:\:\:\:\:\:\: \small + \frac{1}{2}sin 2v_{2}(1+\frac{c^2}{4v_{z}^{2}}cos2v_{2}) ]\end{align*}

So now the total kinetic energy of the system is the sum of mechanical and magnetic energy, which is: $\large K.E = \large K.E_{M} + K.E_{E} \\ \begin{align*}\large \frac{1}{2}Mv_{z}^{2} &= \small \frac{1}{2}mv_{z}^{2} + \frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}}\left\{v_{2}(1 - \frac{c^{2}}{4v_{z}^{2}}) + \frac{1}{2}sin 2v_{2}(1+\frac{c^2}{4v_{z}^{2}}cos2v_{2})\right\} \\ &= \small \frac{1}{2}v_{z}^{2}\left[ m + \frac{\mu Q^2}{8 \pi a}\frac{c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\left\{v_{2}(1 - \frac{c^{2}}{4v_{z}^{2}}) + \frac{1}{2}sin 2v_{2}(1+\frac{c^2}{4v_{z}^{2}}cos2v_{2})\right\}\right] \end{align*} \\ or, \large M = m + \small \frac{\mu Q^2}{8 \pi a}\frac{c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\left\{v_{2}(1 - \frac{c^{2}}{4v_{z}^{2}}) + \frac{1}{2}sin 2v_{2}(1+\frac{c^2}{4v_{z}^{2}}cos2v_{2})\right\}$

So now the total kinetic energy of the system is the sum of mechanical and magnetic energy, which is: $\large K.E = \large K.E_{M} + K.E_{E} \\ \begin{align*}\small \frac{1}{2}Mv_{z}^{2} &= \small \frac{1}{2}mv_{z}^{2} + \frac{\mu Q^2}{16 \pi a}\frac{v_{z}c^{2}}{\sqrt{c^{2}-v_{z}^{2}}} \\ & \small \left\{v_{2}(1 - \frac{c^{2}}{4v_{z}^{2}}) + \frac{1}{2}sin 2v_{2}(1+\frac{c^2}{4v_{z}^{2}}cos2v_{2})\right\} \\ &= \small \frac{1}{2}v_{z}^{2}\large [ \small m + \frac{\mu Q^2}{8 \pi a}\frac{c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}} \\ & \small \left\{v_{2}(1 - \frac{c^{2}}{4v_{z}^{2}}) + \frac{1}{2}sin 2v_{2}(1+\frac{c^2}{4v_{z}^{2}}cos2v_{2})\right\} \large ] \end{align*} \\ \begin{align*}or,\:\:\: \small M &= m + \small \frac{\mu Q^2}{8 \pi a}\frac{c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}} \\ & \small \left\{v_{2}(1 - \frac{c^{2}}{4v_{z}^{2}}) + \frac{1}{2}sin 2v_{2}(1+\frac{c^2}{4v_{z}^{2}}cos2v_{2})\right\}\end{align*}$

So the mass of the object is increased by amount: $\small \frac{\mu Q^2}{8 \pi a}\frac{c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\left\{v_{2}(1 - \frac{c^{2}}{4v_{z}^{2}}) + \frac{1}{2}sin 2v_{2}(1+\frac{c^2}{4v_{z}^{2}}cos2v_{2})\right\}$

So the mass of the object is increased by amount: $\begin{align*} & \small \frac{\mu Q^2}{8 \pi a}\frac{c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}} \\ & \large [ \small v_{2}(1 - \frac{c^{2}}{4v_{z}^{2}}) + \frac{1}{2}sin 2v_{2}(1+\frac{c^2}{4v_{z}^{2}}cos2v_{2}) \large ]\end{align*}$

By evaluating the above extra mass quantity by converting factors sin2v₂ and cos2v₂ in terms of tan and evaluate it using the value of v₂, we get:

\small \frac{\mu Q^2}{8 \pi a}\frac{c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\left\{tan^{-1}\left( \frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}\right)\left(\frac{4v_{z}^{2} -c^{2}}{4v_{z}^{2}}\right) + \frac{(2v_{z}^{2}+c^{2})}{4v_{z}c^{2}}\sqrt{c^{2}-v_{z}^{2}}\right\}

\begin{align*} &\small \frac{\mu Q^2}{8 \pi a}\frac{c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\large [ \small tan^{-1}\left( \frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}}\right)\left(\frac{4v_{z}^{2} -c^{2}}{4v_{z}^{2}}\right) \\ & \small + \frac{(2v_{z}^{2}+c^{2})}{4v_{z}c^{2}}\sqrt{c^{2}-v_{z}^{2}} \large ]\end{align*}

You can see if velocity approaches to that of speed of light (v_z = c), the mass tends to increase to infinity. So it’s velocity will remain constant. So its impossible to increase the velocity of a charged boy more than that of the speed of light in this scenario.

If speed of the object is very very less than that of light,

\begin{align*} & \small \text{the factor} \:\: tan^{-1} \frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}} \text{can be approximated as:} \\ \small &\simeq v_{z}(c^{2}-v_{z}^{2})^{\frac{-1}{2}} - \frac{v_{z}^{3}}{3}(c^{2}-v_{z}^{2})^{\frac{-1}{6}} \:\:\:\:\:\:\: \tiny \text{[Using Maclaurin Series]} \\ \small &\simeq \frac{v_{z}}{c}\left( 1 -\frac{v_{z}^{2}}{c^{2}} \right) ^{-\frac{1}{2}} -\frac{v_{z}^{3}}{3c^{3}}\left( 1 -\frac{v_{z}^{2}}{c^{2}} \right) ^{-\frac{1}{6}} \\ \small &\simeq \frac{v_{z}}{c} - \frac{v_{z}^{3}}{3c^{3}}\left( 1 +\frac{v_{z}^{2}}{6c^{2}} \right) \:\: \tiny \text{[dropping the factor } \frac{v_{z}^{2}}{c^{2}} \text{ in the first term and using Binomial expansion for the second]} \end{align*}

If speed of the object is very very less than that of light,

\begin{align*} & \small \text{the factor} \:\: tan^{-1} \frac{v_{z}}{\sqrt{c^{2}-v_{z}^{2}}} \text{can be approximated as:} \\ \small &\simeq v_{z}(c^{2}-v_{z}^{2})^{\frac{-1}{2}} - \frac{v_{z}^{3}}{3}(c^{2}-v_{z}^{2})^{\frac{-1}{6}} \:\: \tiny \text{[Using Maclaurin Series]} \\ \small &\simeq \frac{v_{z}}{c}\left( 1 -\frac{v_{z}^{2}}{c^{2}} \right) ^{-\frac{1}{2}} -\frac{v_{z}^{3}}{3c^{3}}\left( 1 -\frac{v_{z}^{2}}{c^{2}} \right) ^{-\frac{1}{6}} \\ \small &\simeq \frac{v_{z}}{c} - \frac{v_{z}^{3}}{3c^{3}}\left( 1 +\frac{v_{z}^{2}}{6c^{2}} \right) \\ & \tiny \text{[dropping the factor } \frac{v_{z}^{2}}{c^{2}} \text{ in the first term and using Binomial expansion for the second]} \end{align*}

So the increased mass quantity becomes $\small \frac{\mu Q^2}{8 \pi a}\frac{c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}}\left [\left\{\frac{v_{z}}{c} - \frac{v_{z}^{3}}{3c^{3}}\left( 1 +\frac{v_{z}^{2}}{6c^{2}} \right) \right\}\left(\frac{4v_{z}^{2} -c^{2}}{4v_{z}^{2}}\right) + \frac{(2v_{z}^{2}+c^{2})}{4v_{z}c^{2}}\sqrt{c^{2}-v_{z}^{2}}\right ] \\ \begin{align*} &= \small \frac{\mu Q^2}{8 \pi a}\frac{1}{4v_{z}^{2}\sqrt{1-\frac{v_{z}^{2}}{c^{2}}}}\left[(1 -\frac{v_{z}^{2}}{3c^{2}}-\frac{v_{z}^{4}}{18c^{4}})(4v_{z}^{2}-c^{2}) +(2v_{z}^{2}+c^{2})\sqrt{1-\frac{v_{z}^{2}}{c^{2}}} \right] \\ & \simeq \small \frac{\mu Q^2}{8 \pi a}\frac{1}{4v_{z}^{2}}\left[ 4v_{z}^{2} -\frac{4v_{z}^{4}}{3c^{2}}-\frac{2v_{z}^{6}}{9c^{4}}-c^{2} + \frac{v_{z}^{2}}{3}+\frac{v_{z}^{4}}{18c^{2}} + 2v_{z}^{2} + c^{2} \right] \: \: \: \tiny \text{[By dropping the negligible factor }\sqrt{1-\frac{v_{z}^{2}}{c^{2}}} \text{ ]} \\ &= \frac{\mu}{2 \pi}\frac{Q^{2}}{a}\frac{1}{16}\left[ \frac{19}{3} -\frac{69v_{z}^{2}}{54c^{2}} - \frac{2v_{z}^{4}}{9c^{4}} \right] \\ & \simeq \frac{\mu}{2 \pi}\frac{Q^{2}}{3a}\frac{19}{16} \tiny \:\:\:\:\:\:\:\:\:\:\:\: \text{[Dropping the negligible last two terms]} \\ & \simeq \frac{\mu}{2 \pi}\frac{Q^{2}}{3a}\tiny \:\:\:\:\:\:\:\:\:\:\:\: \text{[As the factor } \frac{19}{16} = 1.18 \text{ is small and will be getting smaller if more terms of approximation is used. So dropped]} \end{align*}$

So the increased mass quantity becomes $\begin{align*} & \small \frac{\mu Q^2}{8 \pi a}\frac{c^{2}}{v_{z}\sqrt{c^{2}-v_{z}^{2}}} \large[ \\ & \:\:\:\:\:\:\: \small \left\{\frac{v_{z}}{c} - \frac{v_{z}^{3}}{3c^{3}}\left( 1 +\frac{v_{z}^{2}}{6c^{2}} \right) \right\}\left(\frac{4v_{z}^{2} -c^{2}}{4v_{z}^{2}}\right) \\ & \:\:\:\:\:\:\: \small + \frac{(2v_{z}^{2}+c^{2})}{4v_{z}c^{2}}\sqrt{c^{2}-v_{z}^{2}} \large \: ] \\ &= \small \frac{\mu Q^2}{8 \pi a}\frac{1}{4v_{z}^{2}\sqrt{1-\frac{v_{z}^{2}}{c^{2}}}}\large [ \small (1 -\frac{v_{z}^{2}}{3c^{2}}-\frac{v_{z}^{4}}{18c^{4}})(4v_{z}^{2}-c^{2}) \\ & \:\:\:\:\:\:\: \small +(2v_{z}^{2}+c^{2})\sqrt{1-\frac{v_{z}^{2}}{c^{2}}} \large \: ] \\ & \simeq \small \frac{\mu Q^2}{8 \pi a}\frac{1}{4v_{z}^{2}}\large [ \small 4v_{z}^{2} -\frac{4v_{z}^{4}}{3c^{2}}-\frac{2v_{z}^{6}}{9c^{4}}-c^{2} + \frac{v_{z}^{2}}{3} \\ & \small \:\:\:\:\:\:\: +\frac{v_{z}^{4}}{18c^{2}} + 2v_{z}^{2} + c^{2} \large \: ] \: \: \: \tiny \text{[By dropping the negligible factor }\sqrt{1-\frac{v_{z}^{2}}{c^{2}}} \text{ ]} \\ &= \frac{\mu}{2 \pi}\frac{Q^{2}}{a}\frac{1}{16}\left[ \frac{19}{3} -\frac{69v_{z}^{2}}{54c^{2}} - \frac{2v_{z}^{4}}{9c^{4}} \right] \\ & \simeq \frac{\mu}{2 \pi}\frac{Q^{2}}{3a}\frac{19}{16} \tiny \:\:\:\:\:\:\:\: \text{[Dropping the negligible last two terms]} \\ & \simeq \frac{\mu}{2 \pi}\frac{Q^{2}}{3a} \:\:\:\: \tiny \text{[As the factor } \frac{19}{16} = 1.18 \text{ is small and will be getting smaller } \\ & \:\:\:\:\:\:\:\: \:\:\:\:\:\:\:\: \:\:\:\:\:\:\:\: \tiny \text{if more terms of approximation is used. So dropped]} \end{align*}$

This is the same factor which we obtained in our pervious analysis without considering any field distortion.

So does this prove that speed of light is the maximum limit to any charged bodies? And what about neutral bodies?

Well that’s not the case. The limit of speed of light is for very limiting condition like the one mentioned here. There are many ways to overcome it. Unfortunately this very specific case for electrodynamics of moving bodies is being misinterpreted and generalized into erroneous theories like relativity without any physical medium.

Will write about it in future post.

The Critical Thinking Hub

Think Beyond the Matrix

Impact on Mass of A Moving Charged Object – Part 2

[When Speed → c]

Leave a Reply Cancel reply